The global economy has expanded at an ever increasing rate during the past century, increasing at a rate of exponential growth. A study done by a Professor of Economics at the University of California at Berkley estimated world GDP increased to $41.016 trillion in 2000 from $1.102 trillion in 1900 – a growth rate of approximately 3.617% per year. While GDP only implies the market value of all good produced, all aspects affecting the economy have been increasing at an exponential rate, from human population growth to agricultural production, to industrial production, consumption of raw materials, and pollution. Nearly all economists and most people view this feat as a positive achievement and they look to continue this same pattern of growth into the foreseeable future. Hardly any are asking if this pattern is sustainable.
First, a word on exponential growth. Exponential growth is a quantity which increases proportionally to what is already there. This is different from linear growth, where a quantity increases at a constant rate over a given period of time. Consider folding a piece of paper measuring .025 cm in thickness. You have just doubled the thickness of the original piece of paper. Fold it again and you have quadrupled the original thickness. Fold it a third time and this piece of paper is 8 times as thick as the original paper, measuring .2 cm. Continue folding until you have done this 30 times and how thick do you think the paper is? The paper is now 268.44 km. How about another ten folds to 40? This paper is now 274,877 km long, over halfway from the earth to the moon. And with one more fold the thickness will pass the moon. Nine more folds, totaling 50 folds from the original thickness and our paper is now 281,474,976 km, well past the distance from the earth to the sun.
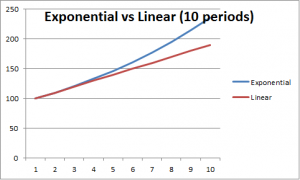
For any quantity to grow exponentially it does not need to double every period, and you can easily calculate an approximate doubling time for a given growth rate. If the original sheet of paper only increased it thickness by 10% every “fold” (or period increase) the approximate doubling time would be 7 folds. This means it will take approximately seven times longer for the thickness to reach the sun, or about 350 folding periods. This is the power of exponential growth. In the short run exponential growth is not much different from linear growth. The impact lies in its long term effects. Now, given that our businesses want to expand their output exponentially, does anybody see a potential problem here?
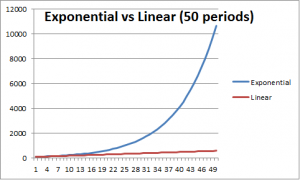
The obvious problem is that we live on a planet with finite space and resources. Consider world metal production which has risen at a rate of 5% historically. In 2008 more than 1.8 billion tons of metal was produced. If this pace were to continue in a little over 700 years the yearly mining output would be greater than the entire mass of the planet. However we would actually mine the weight of the planet in a single year much sooner than this because this figure only refers to the amount of metal produced, not the tonnage of ore needed to be mined to produce the metal, which is much greater. Obviously this can’t happen and just as obvious, this is a problem for our current economic system. As I see it, the question that we need to be asking in our economic and policy debates is what happens when our economic system, which depends on exponential growth, reaches the limits to growth? The only possible answer is that it breaks down.
Further reading: Limits to Growth: The 30-Year Update by Donella Meadows; Collapse by Jared Diamond; One With Nineveh by Paul and Anne Ehrlich